The modulus of elasticity describes a basic mechanical property that defines how a material responds to stress applied to it. In the case of steel, the modulus of elasticity is of significant concern, as there are many applications of steel in the construction, machinery, and industry sectors. This type of knowledge can be used to obtain an approximation of the deformation that a given steel member will undergo upon the application of a load. This ensures the safety of the steel member and optimizes its efficiency within the structure.
What is Modulus of Elasticity in Steel?
The modulus of elasticity of steel, also called Young’s modulus and usually denoted by E, is a measure of how stiff steel is and how much it resists changing shape when a force is applied. In simple terms, it tells us how much a steel member will stretch or compress under a given load. For steel, this value is typically about 200 GPa, which is quite high. That’s why steel doesn’t bend easily and can safely carry heavy loads without deforming too much.
Modulus of Elasticity in Steel Diagram
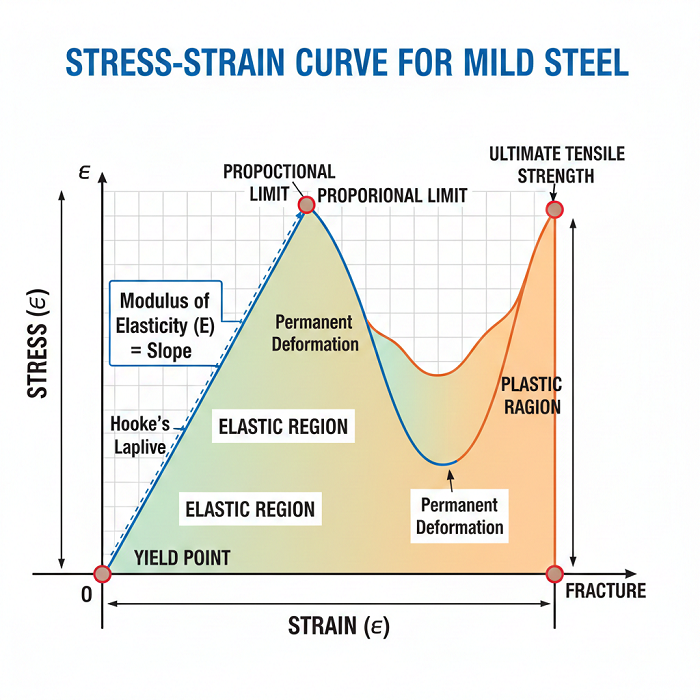
The above figure shows the main areas and points of a stress-strain curve of mild steel used to determine the modulus of elasticity.
Discussion of the Diagram and the Modulus:
-
Elastic Region (O to B): At this stage, the material is at an elastic stage. When the stress is removed, the material will be restored to its original form.
-
Proportional Limit (Point A): It is the location at which the stress is directly proportionate to the strain. Here, Hooke's Law applies. The line here is straight.
-
Modulus of Elasticity (E): The modulus of elasticity, or Young’s modulus, can be considered as the slope of the above-mentioned straight part of the curve from points O to A.
-
Yield Point (Point B): Once the elastic limit or the upper yield strength is crossed, the material starts experiencing plastic deformation; in other words, it won’t return to its original form after the force is removed. Related: What is Yield Point?
-
Plastic Region: It shows the area of permanent deformation where the material undergoes strain hardening and necking until it finally breaks.
Formula and Units of Modulus of Elasticity in Steel
Young's Modulus, E, also known as the Modulus of Elasticity, which describes the stiffness of the material and utilizes the formula E = Stress / Strain (σ/ε), is measured in units of Pressure, such as Gigapascals (GPa), Pascals (Pa), or pounds per square inch (psi). since strain is dimensionless. For steel, this value is usually around 200 GPa (200,000 MPa or 29,000,000 psi), a basically inelastic material.
Real-world Example of Modulus of Elasticity in Steel
The high modulus of elasticity of steel can be seen in skyscrapers. Steel has a modulus of about 200 GP which means it can hold a lot of weight without bending much. As steel is stiff, it is stronger than stone bridges that can hold the same amount of weight and also frequently used in making airplane wings that are strong but bendable. Also, they are stiff so that forces can be moved between them.
Young's Modulus or Modulus of Elasticity—Explained
Young's Modulus (E), or Modulus of Elasticity, or Tensile Modulus, is the measure of the resistance to elastic deformation of a solid substance; it is the ratio of the stress to the strain in the elastic part.
Given by the formula: E=σ/ε
Key Concepts:
-
Stress (σ): The applied force per unit area (e.g., Pascals or N/m²)
-
Strain (ε): The relative deformation, or the change in length divided by the original length (dimensionless).
-
Linear Elastic Region: The range where stress is directly proportional to strain (Hooke's Law).
Related: What is a Stress-Strain Curve?
Modulus of Elasticity of Popular Industrial Materials
The modulus of elasticity (Young’s modulus) shows a material’s elasticity under stress, with similar values ranging from very high to low. Here is a table with typical values in Gigapascals (GPa):
|
Material |
Modulus of Elasticity (Mpsi) |
|
ABS |
0.15–0.39 |
|
Acrylic |
0.41–0.48 |
|
Aluminum |
10 |
|
Copper |
16 |
|
Glass |
10.2 |
|
Magnesium |
6.5 |
|
Nylon |
0.19–0.61 |
|
Polypropylene |
0.16–0.23 |
|
Steel |
29–30 |
|
Titanium |
17 |
|
Diamond |
101.5–174.0 |
Applications of the Modulus of Elasticity in Steel
The modulus of elasticity in steel is a key design parameter that helps engineers predict how steel components will behave under load. It consists of several applications, such as structural engineering, mechanical engineering and machine design, automotive industry, railway engineering, and aerospace and defense.
Structural Engineering
Structural engineering involves the use of the modulus of elasticity for calculating beam deflection, column stability, and load capacity when designing buildings and bridges. Structural engineers also use the modulus of elasticity to help them understand how buildings and bridges will behave when loaded and therefore help them ensure that buildings and bridges do not overbend under any of the various loads and therefore provide for safety as well as comfort.
Mechanical Engineering & Machine Design
Mechanical engineering and machine design use the modulus of elasticity for many purposes, but one of the most important is for holding all the various components of a machine in alignment. Therefore, this property enables smooth operation of the machine, reduces vibration, and extends its lifespan.
Mechanical engineers utilize this property to design machinery and components of machinery so that they will not fail prematurely or require excessive maintenance, and to help to reduce the cost of ownership of machinery and components of machinery.
Automotive Industry
For designing chassis, frames, and suspension components in automotive engineering, the modulus of elasticity of the steel provides a way to regulate stiffness and flexibility in vehicles. Thus, allowing them to withstand shocks and thrust from road loads while providing safe and easy-to-drive vehicles with a comfortable feel for occupants, along with keeping the overall integrity of the vehicle intact.
Railway Engineering
Steel is utilized for railway tracks, wheels, axles, bridges, etc. The elasticity of steel enables engineers to calculate the amount of deflection caused by moving loads on tracks, thus minimizing fatigue failure and maximizing the amount of time a train can be operated safely at high speed and heavy haul for an extended period.
Aerospace & Defense applications
Steel components utilized in the aerospace and defense industries are exposed to and therefore resistant against significant amounts of dynamic loads with very high levels of stress. The elasticity of steel will allow an engineer to fabricate parts that will maintain their strength, dimensional accuracy, and reliability in the most demanding operating environments while avoiding excessive deformation.
Conclusion
The modulus of elasticity is an important physical property of steel that expresses its stiffness and elasticity. There is a high and stable value of steel. Therefore, the high resistance to deformation of steel under a load makes it a common material in structural/engineering projects that are heavily concerned with safety, efficiency, and durability. As such, it is of paramount importance to know the modulus of elasticity to ensure that the engineers come up with systems that will be safe, efficient, and durable.